Los valores y vectores característicos tienen muchas aplicaciones en la tanto en el ramo de las matemáticas como física, mencionaremos algunos temas en donde también se pueden emplear: Orbitales moleculares, Análisis factorial, Tensor de inercia, Tensor de tensión y Valores propios de un grafo, En ecuaciones lineales, matrices, etc.
A continuacion algunas de ellas
Caras propias
En procesado de imagen, las imágenes procesadas de caras pueden verse como vectores cuyas componentes son la luminancia de cada píxel. La dimensión de este espacio vectorial es el número de píxeles. Los vectores propios de la matriz de covarianza asociada a un conjunto amplio de imágenes normalizadas de rostros se llaman caras propias. Son muy útiles para expresar una imagen de un rostro como la combinación lineal de otras. Las caras propias proporcionan un medio de aplicar compresión de datos a los rostros, para propósitos de biometría.
Tensor de inercia
En mecánica, los vectores propios del momento de inercia definen los ejes principales de un cuerpo rígido. El tensor de inercia es necesario para determinar la rotación de un cuerpo rígido alrededor de su centro de masa. Los valores propios definen los momentos máximos y mínimos obtenidos mediante el círculo de Mohr.
Tensor de tensión
En mecánica de sólidos deformables, el tensor de tensión es simétrico, así que puede descomponerse en un tensor diagonal cuyos valores propios en la diagonal y los vectores propios forman una base.
CONCLUSION
los valores y vectores caracteristicos son de vital importancia en muchas ramas de la fisica y las matematicas, sus aplicaciones son muy vaiadas van desde el algebra lineal avanzada,analisis vectorial, pasando por el calculo numerico, el famoso calculo tensorial,el estudio de señales y de imagenes hasta la optica.
Con esto podríamos decir que hemos aprendido a tener un amplio criterio de la utilidad de temas ya vistos en nuestra carrera, ya que no podemos omitir las enseñanzas pasadas ya que estas nos forman las bases para comprender y analizar y poder poner en practica los temas futuros.
viernes, 28 de mayo de 2010
jueves, 27 de mayo de 2010
6.7 Teorema de Cayley-Hamilton
En álgebra lineal, el teorema de Cayley-Hamilton (que lleva los nombres de los matemáticos Arthur Cayley y William Hamilton) asegura que todo endomorfismo de un espacio vectorial de dimensión finita sobre un cuerpo cualquiera anula su propio polinomio característico.
En términos matriciales, eso significa que :
si A es una matriz cuadrada de orden n y si

es su polinomio característico (polinomio de indeterminada X), entonces al sustituir formalmente X por la matriz A en el polinomio, el resultado es la matriz nula:

El teorema de Cayley-Hamilton se aplica también a matrices cuadradas de coeficientes en un anillo conmutativo cualquiera.
Un corolario importante del teorema de Cayley-Hamilton afirma que el polinomio mínimo de una matriz dada es un divisor de su polinomio característico, y no solo eso, el polinomio mínimo tiene los mismos factores irreducibles que el polinomio característico.Toda matriz cuadrada satisface su propia ecuación característica. Es decir, si p(λ) = 0 es la ecuaciσn característica de A, entonces p(λ) = 0 .
El teorema de Cayley-Hamilton es una herramienta matematica poderosa, ya que permite
obtener con mayor facilidad el calculo de e^At con un esfuerzo mucho menor comparado con Laplace o el metodo de eigevalores, ademas funciona para calcular funciones matriciales en general.
Este teorema tiene dos familias de uso:
Permite establecer resultados teóricos, por ejemplo para calcular el polinomio característico de un endomorfismo nilpotente.
Permite también simplificaciones poderosas en el cálculo de matrices. La aproximación por polinomios mínimos es en general menos costosa que la que se hace por determinantes.
Encontramos este teorema utilizado en los artículos sobre los polinomios de endomorfismo, endomorfismos nilpotentes, y más en general en la teoría general de las matrices
Ejemplo:
Consideremos por ejemplo la matriz:

El polinomio característico se escribe

El teorema de Cayley-Hamilton afirma que:
A^2 − 5A − 2I2 = 0
y esta relación puede verificarse inmediatamente en ese caso. Además el teorema de Cayley-Hamilton permite calcular las potencias de una matriz de modo más sencillo que por un cálculo directo. Tomemos la relación anterior
A^ − 5A − 2I2 = 0
A^ = 5A + 2I2
Así, por ejemplo, para calcular A^4, podemos escribir
A^8 = (5A + 2I2)A = 5A2 + 2A = 5(5A + 2I2) + 2A = 27A + 10I2
y llegamos a
A^4 = A^83A = (27A + 10I2)A = 27A^2 + 10A = 27(5A + 2I2) + 10A
A^4 = 145A + 54I2.
Podemos utilizar también la relación polinomial inicial A2 − 5A − 2I2 = 0 para probar la inversibilidad de A y calcular su inverso. En efecto, basta con factorizar una potencia de A donde sea posible y
A(A − 5I) = 2I2
lo que demuestra que A admite como inverso

En algunas situaciones el teorema de Caley – Hamilton es útil para calcular la inversa de una matriz. Si existe A-1 y p(A) = 0, entonces A-1 p(A) = 0.para ilustrar esto, si p(λ) = λn + an-1 λn-1 + … + a1λ + a0, entonces
p(A) = An + an-1 An-1 + …+ a1A + a0I = 0
y
A-1p(A) = An-1 + an-1An-2 + … + a2A + a1I + a0A-1 = 0
Asi
A-1 = 1/a0 (-An-1 -an-1An-2 - … - a2A – a1I )
Observe que a0 es diferente de 0 porque a0 = det A (¿Por qué?) y se supuso que A era invertible.
1 −1 4
Ejemplo 2: Aplicación del teorema de Caley – Hamilton para calcular A-1 Sea A = 3 2 −1
1 −1
Entonces p(λ) = λ3 - 2λ2 - 5λ + 6. Aquí n = 3, a2 = −2,a1 = −5, a0 = 6 y A-1 = 1/6 (-A2 + 2A + 5I)
-6 −1 −1 2 −2 8 5 0 0
= 1/6 −7 0 −11 + 6 4 −2 + 0 5 0
-3 1 −8 4 2 −2 0 0 5
1 −3 7
= 1/6 −1 9 −13
1 3 −5
En términos matriciales, eso significa que :
si A es una matriz cuadrada de orden n y si

es su polinomio característico (polinomio de indeterminada X), entonces al sustituir formalmente X por la matriz A en el polinomio, el resultado es la matriz nula:

El teorema de Cayley-Hamilton se aplica también a matrices cuadradas de coeficientes en un anillo conmutativo cualquiera.
Un corolario importante del teorema de Cayley-Hamilton afirma que el polinomio mínimo de una matriz dada es un divisor de su polinomio característico, y no solo eso, el polinomio mínimo tiene los mismos factores irreducibles que el polinomio característico.Toda matriz cuadrada satisface su propia ecuación característica. Es decir, si p(λ) = 0 es la ecuaciσn característica de A, entonces p(λ) = 0 .
El teorema de Cayley-Hamilton es una herramienta matematica poderosa, ya que permite
obtener con mayor facilidad el calculo de e^At con un esfuerzo mucho menor comparado con Laplace o el metodo de eigevalores, ademas funciona para calcular funciones matriciales en general.
Este teorema tiene dos familias de uso:
Permite establecer resultados teóricos, por ejemplo para calcular el polinomio característico de un endomorfismo nilpotente.
Permite también simplificaciones poderosas en el cálculo de matrices. La aproximación por polinomios mínimos es en general menos costosa que la que se hace por determinantes.
Encontramos este teorema utilizado en los artículos sobre los polinomios de endomorfismo, endomorfismos nilpotentes, y más en general en la teoría general de las matrices
Ejemplo:
Consideremos por ejemplo la matriz:

El polinomio característico se escribe

El teorema de Cayley-Hamilton afirma que:
A^2 − 5A − 2I2 = 0
y esta relación puede verificarse inmediatamente en ese caso. Además el teorema de Cayley-Hamilton permite calcular las potencias de una matriz de modo más sencillo que por un cálculo directo. Tomemos la relación anterior
A^ − 5A − 2I2 = 0
A^ = 5A + 2I2
Así, por ejemplo, para calcular A^4, podemos escribir
A^8 = (5A + 2I2)A = 5A2 + 2A = 5(5A + 2I2) + 2A = 27A + 10I2
y llegamos a
A^4 = A^83A = (27A + 10I2)A = 27A^2 + 10A = 27(5A + 2I2) + 10A
A^4 = 145A + 54I2.
Podemos utilizar también la relación polinomial inicial A2 − 5A − 2I2 = 0 para probar la inversibilidad de A y calcular su inverso. En efecto, basta con factorizar una potencia de A donde sea posible y
A(A − 5I) = 2I2
lo que demuestra que A admite como inverso

En algunas situaciones el teorema de Caley – Hamilton es útil para calcular la inversa de una matriz. Si existe A-1 y p(A) = 0, entonces A-1 p(A) = 0.para ilustrar esto, si p(λ) = λn + an-1 λn-1 + … + a1λ + a0, entonces
p(A) = An + an-1 An-1 + …+ a1A + a0I = 0
y
A-1p(A) = An-1 + an-1An-2 + … + a2A + a1I + a0A-1 = 0
Asi
A-1 = 1/a0 (-An-1 -an-1An-2 - … - a2A – a1I )
Observe que a0 es diferente de 0 porque a0 = det A (¿Por qué?) y se supuso que A era invertible.
1 −1 4
Ejemplo 2: Aplicación del teorema de Caley – Hamilton para calcular A-1 Sea A = 3 2 −1
1 −1
Entonces p(λ) = λ3 - 2λ2 - 5λ + 6. Aquí n = 3, a2 = −2,a1 = −5, a0 = 6 y A-1 = 1/6 (-A2 + 2A + 5I)
-6 −1 −1 2 −2 8 5 0 0
= 1/6 −7 0 −11 + 6 4 −2 + 0 5 0
-3 1 −8 4 2 −2 0 0 5
1 −3 7
= 1/6 −1 9 −13
1 3 −5
6.6 Formas cuadraticas
Una forma cuadrática es una aplicación del espacio vectorial E en el cuerpo K, que cumple las siguientes condiciones equivalentes: a) Existe una forma bilineal simétrica f de ExE en el cuerpo K tal que (x) = f(x,x). A f se le llama forma polar de . b) (lx) = l2x, . Además f(x,y) = ( (x + y) " (x) " (y)) / 2 es una forma bilineal simétrica definida en ExE y con valores en K. A se la llama forma cuadrática asociada a f. Cuando se dice que la forma cuadrática es real. A veces a las formas cuadráticas definidas positivas se las denomina métricas. Formas cuadráticas Una forma cuadrática en R3 es cualquier conjunto de puntos xT=(x1,x2,x3) que satisface una ecuación del tipo: xTAx=r, (1) donde A es una matriz simétrica de 3x3 a coeficientes reales y r es un número real. Vía una rotación del espacio dada por y=PTx donde yT=(y1,y2,y3) y P es una matriz unitaria de 3x3 a coeficientes reales, se puede expresar una forma cuadrática arbitraria con respecto a un vector y de manera que: yTDy=r, (2) donde D es una matriz diagonal de 3x3 a coeficientes reales. ¿Porqué siempre pueden encontrarse P y D con las propiedades requeridas? ¿Por qué P representa una rotación del espacio? Vía un re-escalamiento adicional dado por z=D'y donde zT=(z1,z2,z3) y D' es una matriz diagonal de 3x3 a coeficientes reales no-negativos, se puede expresar la última ecuación obtenida con respecto el vector z de manera que quede representada por una ecuación del tipo: zTJz=r, (3) donde J es una matriz diagonal de 3x3 que sólo puede contener en su diagonal valores que están en {"1,0,1}.
Una forma cuadrática es una aplicación del espacio vectorial E en el cuerpo K, que cumple las siguientes condiciones equivalentes:
a) Existe una forma bilineal simétrica f de ExE en el cuerpo K tal que (x)=f(x,x). A f se le llama forma polar de .
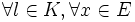
b) (lx) = l2x
Además f(x,y) = ( (x + y) " (x) " (y)) / 2 es una forma bilineal simétrica definida en ExE y con valores en K. A se la llama forma cuadrática asociada a f.
Cuando K = R
se dice que la forma cuadrática es real. A veces a las formas cuadráticas definidas positivas se las denomina métricas.
Una forma cuadrática es una aplicación del espacio vectorial E en el cuerpo K, que cumple las siguientes condiciones equivalentes:
a) Existe una forma bilineal simétrica f de ExE en el cuerpo K tal que (x)=f(x,x). A f se le llama forma polar de .
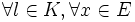
b) (lx) = l2x
Además f(x,y) = ( (x + y) " (x) " (y)) / 2 es una forma bilineal simétrica definida en ExE y con valores en K. A se la llama forma cuadrática asociada a f.
Cuando K = R
se dice que la forma cuadrática es real. A veces a las formas cuadráticas definidas positivas se las denomina métricas.
6.5 Diagonalizacion de matrices simetricas, diagonalizacion ortogonal
Dada A una matriz simétrica asociada a f, endomorfismo de Rn, se verifican las siguientes
propiedades:
Teorema 1. Sea A una matriz simétrica real de n x n. Entonces los valores característicos de A son reales.
Teorema 2. Sea A una matriz simétrica real de n x n. Si λ1 y λ2 son valores característicos distintos con correspondientes vectores característicos reales v1 y v2, entonces v1 y v2 son ortogonales.
Teorema 3.Sea A una matriz simétrica real de n x n. Resulta entonces que A tiene n vectores característicos reales ortonormales.
Obervación. Se concluye de este teorema que la multiplicidad geométrica de cada valor característico de A es igual a su multiplicidad algebraica.
El Teorema 3 nos dice que si A es simétrica entonces Rn tiene una base B = {u1, u2, ... un} que consiste de vectores característicos ortonormales de A. Sea Q la matriz cuyas columnas u1, u2, ... un. Entonces Q es una matriz ortogonal. Esto nos conduce hacia la siguiente definición.
Una matriz diremos que es ortogonal si su traspuesta coincide con su inversa.

Definicion. Matriz ortogonalmente diagonizable. Una matriz A de n x n se dice que es diagonalizable ortogonalmente si existe una matriz ortogonal Q tal que
Q'AQ = D (1)
donde D = diag(λ1, λ2, ..., λn) y λ1, λ2, ..., λn son los valores característicos de A.
Teorema 4. Sea A una matriz real de n x n. Entonces A es diagonalizable ortogonalmente si y sólo si A es simétrica.
Procedimiento para encontrar una matriz diagonalizante Q:
i. Encuentre una base para cada espacio característico de A.
ii. Encuentre una base ortonormal para cada espacio característico de A, usando el procedimiento Gram-Schmidt.
iii. Establezca a Q como la matriz cuyas columnas son los vectores característicos ortonormales obtenidos en el paso (ii).
Entre las aplicaciones de la diagonalización de matrices cuadradas se encuentra el análisis de la solución de un sistema dinámico a lo largo del tiempo. Un sistema se caracteriza por el estado de las n variables
que lo determinan y se puede representar por un vector x de Rn cuyas componentes expresan los valores de esas variables.
Ejemplo:


propiedades:
Teorema 1. Sea A una matriz simétrica real de n x n. Entonces los valores característicos de A son reales.
Teorema 2. Sea A una matriz simétrica real de n x n. Si λ1 y λ2 son valores característicos distintos con correspondientes vectores característicos reales v1 y v2, entonces v1 y v2 son ortogonales.
Teorema 3.Sea A una matriz simétrica real de n x n. Resulta entonces que A tiene n vectores característicos reales ortonormales.
Obervación. Se concluye de este teorema que la multiplicidad geométrica de cada valor característico de A es igual a su multiplicidad algebraica.
El Teorema 3 nos dice que si A es simétrica entonces Rn tiene una base B = {u1, u2, ... un} que consiste de vectores característicos ortonormales de A. Sea Q la matriz cuyas columnas u1, u2, ... un. Entonces Q es una matriz ortogonal. Esto nos conduce hacia la siguiente definición.
Una matriz diremos que es ortogonal si su traspuesta coincide con su inversa.

Definicion. Matriz ortogonalmente diagonizable. Una matriz A de n x n se dice que es diagonalizable ortogonalmente si existe una matriz ortogonal Q tal que
Q'AQ = D (1)
donde D = diag(λ1, λ2, ..., λn) y λ1, λ2, ..., λn son los valores característicos de A.
Teorema 4. Sea A una matriz real de n x n. Entonces A es diagonalizable ortogonalmente si y sólo si A es simétrica.
Procedimiento para encontrar una matriz diagonalizante Q:
i. Encuentre una base para cada espacio característico de A.
ii. Encuentre una base ortonormal para cada espacio característico de A, usando el procedimiento Gram-Schmidt.
iii. Establezca a Q como la matriz cuyas columnas son los vectores característicos ortonormales obtenidos en el paso (ii).
Entre las aplicaciones de la diagonalización de matrices cuadradas se encuentra el análisis de la solución de un sistema dinámico a lo largo del tiempo. Un sistema se caracteriza por el estado de las n variables
que lo determinan y se puede representar por un vector x de Rn cuyas componentes expresan los valores de esas variables.
Ejemplo:


6.4 DIAGONALIZACION DE MATRICES, POTENCIAS Y RAICES DE MATRICES
En álgebra lineal, una matriz diagonal es una matriz cuadrada en que las entradas son todas nulas salvo en la diagonal principal, y éstas pueden ser nulas o no. Así, la matriz D = (di,j) es diagonal si:
Para estudiar una matriz suele ser conveniente expresarla de forma lo más sencilla posible. Diagonalizar una matriz A es precisamente eso: escribirla de manera simple encontrando una matriz invertible P y una diagonal D (si se puede).Diagonalizar una matriz es muy importante en el Álgebra Lineal, pues se cumple lo siguiente:

facilitando mucho el calculo de las potencias de A, dado que sieno D una matriz diagonal el calculo de su p-esima potencia es muy sencillo:

La matriz P se llama matriz de paso.
Puede que esto, al principio, no parezca más simple de lo que ya era A directamente. Sin embargo, lo es desde muchos puntos de vista. Dado que las matrices suelen usarse para representar aplicaciones lineales, la expresión anterior puede verse como un cambio de base de la aplicación representada por A; entonces, esta forma de escribirlo dice: hay una base en la que la aplicación lineal A tiene una forma muy simple (diagonal). Esto es útil, por ejemplo, para clasificar una aplicación lineal y estudiar sus propiedades. Las matrices se usan para representar otras cosas como cónicas, cuádricas o formas bilineales, y en estos casos también resulta útil esta forma de expresarlas.
La relación anterior entre las matrices A y D es importante y aparece en muchos contextos, así que tiene nombre propio:
Cuando dos matrices cuadradas A y B verifican que A = P B P-1 para cierta matriz cuadrada P (invertible, claro) decimos que A y B son semejantes.
Una matriz es diagonalizable cuando se puede diagonalizar; es decir, cuando podemos encontrar una matriz diagonal y una invertible de forma que la matriz se escriba como dijimos antes. Dicho de otra forma: una matriz es diagonalizable cuando es semejante a una matriz diagonal.Entonces, más exactamente: una matriz es diagonalizable cuando es semejante a una matriz diagonal real.
¿Cuándo y cómo podemos diagonalizar una matriz?
Si conseguimos escribir una matriz A como A = P D P-1 , entonces podemos poner también A P = P D. Si D es diagonal y nos fijamos en la columna i de esta última igualdad lo que tenemos es que A xi = λi xi (donde xi es la columna i de A y λi es el número en el lugar i de la diagonal de D). Esto nos dice que para diagonalizar una matriz nos hace falta conocer los vectores a los que les pase algo así. Estos vectores también tienen nombre:
Si un número λ y un vector no nulo x verifican la relación A x = λ x diremos queλ es un valor propio o autovalor de la matriz A y que x es un vector propio o autovector de A asociado al valor propio λ.
Es fácil ver que diagonalizar una matriz A de tamaño n×n es lo mismo que encontrar n vectores propios linealmente independientes asociados a valores propios reales, ya que entonces podemos ponerlos por columnas y conseguir así la matriz P (puedes comprobar que entonces se cumple la relación que buscamos). Entonces, para diagonalizar una matriz lo que tenemos que hacer es buscar n vectores propios suyos linealmente independientes asociados a valores propios reales.
¿Cómo encontrar valores y vectores propios de una matriz?
Es fundamental, pues, hallar los valores propios de A y los vectores propios asociados. Como un vector propio l hace que el sistema Ax = λx tenga solución x distinta de cero, la matriz de coeficientes A −λI (donde I denota la matriz identidad de orden n) debe tener determinante no nulo. Este determinante det(A−λI) es un polinomio en λ de grado n y se denomina polinomio característico de A. Por lo tanto, los valores propios de A serán los ceros del polinomio característico de A.
Observa que una matriz puede perfectamente tener valores propios imaginarios.
Por otro lado, el conjunto de vectores propios de A asociados a un mismo valor propio λ forman un subespacio vectorial de Rn que se llama subespacio propio asociado al valor propio λ, y es el núclea de la matriz A −λI. Para concluir si una matriz A es o no diagonalizable bastará pues averiguar si hay "suficientes" valores propios reales para construir D y si hay"suficientes" vectores propios linealmente independientes asociados; esta información nos la dará la dimensión de los subespacios propios y queda recogida en el siguiente resultado:
Una matriz real cuadrada de orden n es diagonalizable si y sólo si tiene n vectores propios linealmente independientes asociados a valores propios reales.
Además, el teorema espectral nos confirma un caso en el que siempre es posible diagonalizar:
Toda matriz real simétrica es diagonalizable.
En este caso,se puede conseguir además que las columnas de la matriz de paso P sean una base ortonormal y por lo tanto que P sea una matriz ortogonal.
El determinante de una matriz coincide con el de su traspuesta
Det A=Det At , es decir, o denotando cada fila con el color usual en esta unidad,
Por tanto, todas las propiedades vistas para las filas de una matriz son también ciertas para sus columnas En la escena, se presenta a la izquierda el determinante de una matriz, y a la derecha, el de su traspuesta. Si variamos los valores de a, b, c, y d, es difícil ver que ambos paralelogramos coinciden. Veremos primero, geométricamente, que coinciden cuando la matriz es triangular.
EJEMPLO, Diagonalizar una matriz" se reduce a encontrar sus vectores y valores propios. Tomemos la matriz:

veamos que es diagonalizable:
Esta matriz tiene los valores propios: λ1 = -1, λ2 = 4
Así A es una matriz 2 por 2 con 2 valores propios diferentes, entonces se dice que es diagonizable.Si queremos diagonalizar A necesitamos calcular los correspondientes vectores propios. Ellos son:

Uno podría verificar fácilmente esto mediande:

Ahora, es la matriz invertible con los vectores propios de como columnas
 con inversa
con inversa

Hallemos ahora la matriz diagonal, usando esta matriz P como sigue:

Realizamos el cálculo introduciendo los datos

Luego resulta que existen matrices P y D tales que

Cumpliendo P y D los requisitos pedidos al principio y por lo tanto la matriz A es diagonizable.
Potencias de una matriz diagonizable
Podemos calcular, por ejemplo, la séptima potencia de la matriz anterior:

Para estudiar una matriz suele ser conveniente expresarla de forma lo más sencilla posible. Diagonalizar una matriz A es precisamente eso: escribirla de manera simple encontrando una matriz invertible P y una diagonal D (si se puede).Diagonalizar una matriz es muy importante en el Álgebra Lineal, pues se cumple lo siguiente:

facilitando mucho el calculo de las potencias de A, dado que sieno D una matriz diagonal el calculo de su p-esima potencia es muy sencillo:

La matriz P se llama matriz de paso.
Puede que esto, al principio, no parezca más simple de lo que ya era A directamente. Sin embargo, lo es desde muchos puntos de vista. Dado que las matrices suelen usarse para representar aplicaciones lineales, la expresión anterior puede verse como un cambio de base de la aplicación representada por A; entonces, esta forma de escribirlo dice: hay una base en la que la aplicación lineal A tiene una forma muy simple (diagonal). Esto es útil, por ejemplo, para clasificar una aplicación lineal y estudiar sus propiedades. Las matrices se usan para representar otras cosas como cónicas, cuádricas o formas bilineales, y en estos casos también resulta útil esta forma de expresarlas.
La relación anterior entre las matrices A y D es importante y aparece en muchos contextos, así que tiene nombre propio:
Cuando dos matrices cuadradas A y B verifican que A = P B P-1 para cierta matriz cuadrada P (invertible, claro) decimos que A y B son semejantes.
Una matriz es diagonalizable cuando se puede diagonalizar; es decir, cuando podemos encontrar una matriz diagonal y una invertible de forma que la matriz se escriba como dijimos antes. Dicho de otra forma: una matriz es diagonalizable cuando es semejante a una matriz diagonal.Entonces, más exactamente: una matriz es diagonalizable cuando es semejante a una matriz diagonal real.
¿Cuándo y cómo podemos diagonalizar una matriz?
Si conseguimos escribir una matriz A como A = P D P-1 , entonces podemos poner también A P = P D. Si D es diagonal y nos fijamos en la columna i de esta última igualdad lo que tenemos es que A xi = λi xi (donde xi es la columna i de A y λi es el número en el lugar i de la diagonal de D). Esto nos dice que para diagonalizar una matriz nos hace falta conocer los vectores a los que les pase algo así. Estos vectores también tienen nombre:
Si un número λ y un vector no nulo x verifican la relación A x = λ x diremos queλ es un valor propio o autovalor de la matriz A y que x es un vector propio o autovector de A asociado al valor propio λ.
Es fácil ver que diagonalizar una matriz A de tamaño n×n es lo mismo que encontrar n vectores propios linealmente independientes asociados a valores propios reales, ya que entonces podemos ponerlos por columnas y conseguir así la matriz P (puedes comprobar que entonces se cumple la relación que buscamos). Entonces, para diagonalizar una matriz lo que tenemos que hacer es buscar n vectores propios suyos linealmente independientes asociados a valores propios reales.
¿Cómo encontrar valores y vectores propios de una matriz?
Es fundamental, pues, hallar los valores propios de A y los vectores propios asociados. Como un vector propio l hace que el sistema Ax = λx tenga solución x distinta de cero, la matriz de coeficientes A −λI (donde I denota la matriz identidad de orden n) debe tener determinante no nulo. Este determinante det(A−λI) es un polinomio en λ de grado n y se denomina polinomio característico de A. Por lo tanto, los valores propios de A serán los ceros del polinomio característico de A.
Observa que una matriz puede perfectamente tener valores propios imaginarios.
Por otro lado, el conjunto de vectores propios de A asociados a un mismo valor propio λ forman un subespacio vectorial de Rn que se llama subespacio propio asociado al valor propio λ, y es el núclea de la matriz A −λI. Para concluir si una matriz A es o no diagonalizable bastará pues averiguar si hay "suficientes" valores propios reales para construir D y si hay"suficientes" vectores propios linealmente independientes asociados; esta información nos la dará la dimensión de los subespacios propios y queda recogida en el siguiente resultado:
Una matriz real cuadrada de orden n es diagonalizable si y sólo si tiene n vectores propios linealmente independientes asociados a valores propios reales.
Además, el teorema espectral nos confirma un caso en el que siempre es posible diagonalizar:
Toda matriz real simétrica es diagonalizable.
En este caso,se puede conseguir además que las columnas de la matriz de paso P sean una base ortonormal y por lo tanto que P sea una matriz ortogonal.
El determinante de una matriz coincide con el de su traspuesta
Det A=Det At , es decir, o denotando cada fila con el color usual en esta unidad,
Por tanto, todas las propiedades vistas para las filas de una matriz son también ciertas para sus columnas En la escena, se presenta a la izquierda el determinante de una matriz, y a la derecha, el de su traspuesta. Si variamos los valores de a, b, c, y d, es difícil ver que ambos paralelogramos coinciden. Veremos primero, geométricamente, que coinciden cuando la matriz es triangular.
EJEMPLO, Diagonalizar una matriz" se reduce a encontrar sus vectores y valores propios. Tomemos la matriz:

veamos que es diagonalizable:
Esta matriz tiene los valores propios: λ1 = -1, λ2 = 4
Así A es una matriz 2 por 2 con 2 valores propios diferentes, entonces se dice que es diagonizable.Si queremos diagonalizar A necesitamos calcular los correspondientes vectores propios. Ellos son:

Uno podría verificar fácilmente esto mediande:

Ahora, es la matriz invertible con los vectores propios de como columnas
 con inversa
con inversa 
Hallemos ahora la matriz diagonal, usando esta matriz P como sigue:

Realizamos el cálculo introduciendo los datos

Luego resulta que existen matrices P y D tales que

Cumpliendo P y D los requisitos pedidos al principio y por lo tanto la matriz A es diagonizable.
Potencias de una matriz diagonizable
Podemos calcular, por ejemplo, la séptima potencia de la matriz anterior:

6.3 Determinacion delos valores y vectores caracteristicos de una matriz cuadrada
Cálculo de valores propios y vectores propios
Si se quiere calcular los valores propios de una matriz dada y ésta es pequeña, se puede calcular simbólicamente usando el polinomio característico. Sin embargo, a menudo resulta imposible para matrices extensas, caso en el que se debe usar un método numérico.
Encontrando valores propios
Una herramienta importante para encontrar valores propios de matrices cuadradas es el polinomio característico: decir que λ es un valor propio de A es equivalente a decir que el sistema de ecuaciones lineales (A - λI) v = 0 (donde I es la matriz identidad) tiene una solución no nula v (un vector propio), y de esta forma es equivalente al determinante: det(A- λI) = 0
La función p(λ) = det(A - λI) es un polinomio de λ pues los determinante se definen como sumas de productos. Éste es el polinomio característico de A: los valores propios de una matriz son los ceros de su polinomio característico.
Todos los valores propios de una matriz A pueden calcularse resolviendo la ecuación pA(λ) = 0.
Si A es una matriz n×n, entonces pA tiene grado n y A tiene como máximo n valores propios.
Encontrando vectores propios
Una vez que se conocen los valores propios λ, los vectores propios se pueden hallar resolviendo el sistema de ecuaciones homogéneo
(A - λI)V = 0
Un ejemplo de matriz sin valores propios reales es la rotación de 90 grados en el sentido de las manecillas del reloj

cuyo polinomio caracteristico es -λ^2 - 1 y sus valores propios son el par de conjugados complejos i, -i. Los vectores propios asociados tampoco son reales.
Considérese la matriz:

que representa un operador lineal R³ ! R³. Si se desea computar todos los valores propios de A, se podría empezar determinando el polinomio característico


Si se quiere calcular los valores propios de una matriz dada y ésta es pequeña, se puede calcular simbólicamente usando el polinomio característico. Sin embargo, a menudo resulta imposible para matrices extensas, caso en el que se debe usar un método numérico.
Encontrando valores propios
Una herramienta importante para encontrar valores propios de matrices cuadradas es el polinomio característico: decir que λ es un valor propio de A es equivalente a decir que el sistema de ecuaciones lineales (A - λI) v = 0 (donde I es la matriz identidad) tiene una solución no nula v (un vector propio), y de esta forma es equivalente al determinante: det(A- λI) = 0
La función p(λ) = det(A - λI) es un polinomio de λ pues los determinante se definen como sumas de productos. Éste es el polinomio característico de A: los valores propios de una matriz son los ceros de su polinomio característico.
Todos los valores propios de una matriz A pueden calcularse resolviendo la ecuación pA(λ) = 0.
Si A es una matriz n×n, entonces pA tiene grado n y A tiene como máximo n valores propios.
Encontrando vectores propios
Una vez que se conocen los valores propios λ, los vectores propios se pueden hallar resolviendo el sistema de ecuaciones homogéneo
(A - λI)V = 0
Un ejemplo de matriz sin valores propios reales es la rotación de 90 grados en el sentido de las manecillas del reloj

cuyo polinomio caracteristico es -λ^2 - 1 y sus valores propios son el par de conjugados complejos i, -i. Los vectores propios asociados tampoco son reales.
Considérese la matriz:

que representa un operador lineal R³ ! R³. Si se desea computar todos los valores propios de A, se podría empezar determinando el polinomio característico


6.2 Polinomio y ecuacion caracteristica
Para calcular eigenvalores de una matriz de transformación se usa la definición de eigenvectores el
cual es:
Av = λv
El miembro derecho queda idéntico cuando lo multiplicamos por la matriz identidad:
Av = Iλv
Así la primera ecuación queda:
Av = Iλv
Entonces:
Av - Iλv = (A - Iλ)v = 0
De este modo:
A - λI = O
El determinante del primer miembro es un polinomio en términos de λ,el cual tiene el nombre de polinomio caracteristico de A, el cual es:
Det[A - λ]
Asi mismo llamamos a
Det[A - λ] = 0
ecuación característica de A, la cual nos da los eigenvalores de la matriz A.
Ejemplo:
Determinar el polinomio y la ecuacion caracteristica de la siguiente matriz:

El polinomio característico viene dado por la expresión
Det[A - Iλ]
Entonces


El polinomio caracteristico es λ^2 - λ + 4
y la ecuacion caracteristica es λ^2 - λ + 4 = 0
cual es:
Av = λv
El miembro derecho queda idéntico cuando lo multiplicamos por la matriz identidad:
Av = Iλv
Así la primera ecuación queda:
Av = Iλv
Entonces:
Av - Iλv = (A - Iλ)v = 0
De este modo:
A - λI = O
El determinante del primer miembro es un polinomio en términos de λ,el cual tiene el nombre de polinomio caracteristico de A, el cual es:
Det[A - λ]
Asi mismo llamamos a
Det[A - λ] = 0
ecuación característica de A, la cual nos da los eigenvalores de la matriz A.
Ejemplo:
Determinar el polinomio y la ecuacion caracteristica de la siguiente matriz:

El polinomio característico viene dado por la expresión
Det[A - Iλ]
Entonces


El polinomio caracteristico es λ^2 - λ + 4
y la ecuacion caracteristica es λ^2 - λ + 4 = 0
Suscribirse a:
Entradas (Atom)